Source – engineering.com
The ocean is indeed a strange place, but Whitman might not have found it quite so confounding if he’d had access to deep learning. This technology is allowing machines to do everything from disease diagnosis to musical composition to playing video games. Now, a team of scientists and engineers at the IBM Research lab in Dublin have set deep learning on that harshest of mistresses: the sea.
Their deep-learning framework for simulating ocean waves enables real-time wave condition forecasts for a fraction of the traditional computational cost. ENGINEERING.com had the opportunity to discuss this new approach with Fearghal O’Donncha, research scientist at IBM Research – Ireland.
How are wave forecasts traditionally calculated?
Traditionally, wave forecasting has been done by solving a set of partial differential equations that describe the fundamental physics of wave propagation. All information on sea-state conditions are contained in the wave energy density, distributing wave energy over frequencies and propagation direction (essentially it’s solving for the transport of energy). The evolution of wave energy is computed by solving the spectral action-balance equation in space and time.
Why does this approach require High Performance Computing (HPC)?
The above equations cannot be solved directly and instead are discretized onto a computational grid and solved numerically using highly optimized linear algebra solvers.
Typically, the Finite Element Method (FEM) is used to discretize onto a computational mesh and propagated forward in time in a timestepping approach. Accurately resolving wave conditions in coastal regions subject to large variations in water depth requires high resolution discretization in space (and consequently smaller timesteps). This results in a dense computational mesh on which the propagation of wave conditions must be resolved at every computational timestep.
So, how does the deep-learning approach reduce computational requirements so drastically [by 12,000 percent] without affecting forecast accuracy?
The deep-learning approach is a complete paradigm shift from the physics based approach described above.
Traditionally, a rule-based approach is adopted, where information on the evolution of wave energy is explicitly coded into the computational model. The deep-learning approach is more of a “black-box” model. It uses the same mathematical fundamentals that are used in image processing software—such as facial recognition or learning consumer preferences for advertising. The deep learning approach does not contain any information on wave physics.
Instead, it’s fed a huge number of labelled images representing spatial maps of wave conditions for the region. It then learns a relationship between these images and the inputs to the model (wind speeds, ocean currents, etc.) and by processing many, many images, it learns to make inferences or predictions on future wave conditions.
Does this approach make it possible improve the accuracy of forecasts as well, or is this purely about reducing computational demands?
In recent years, there has been huge advances made in machine learning in areas such as language processing, image recognition and the ability to mimic many human tasks. With the success of this initial approach, the opportunity exists to translate these advances from other spheres (that rely on highly complex machine learning techniques) to wave forecasting and to the geosciences in general.
These provide exciting scope to gain very high accuracy forecasts while still maintaining very lightweight computational demands.
What were the biggest engineering challenges you faced in developing this deep-learning framework?
The biggest challenges were: (1) obtaining sufficient data to train the machine learning model and (2) selecting the most appropriate topology for the machine learning model.
Machine learning approaches learn relationships by being fed huge volumes of labelled data. In the geosciences, sufficient volumes of data typically do not exist. Hence, we adopted the novel approach of using a validated, physics based Simulating WAves Nearshore (SWAN) model to generate training data for the machine learning model. This required running the SWAN model with realistic input data (data extracted from The Weather Company (TWC) and from operational wave and current models from NOAA and UCLA respectively).
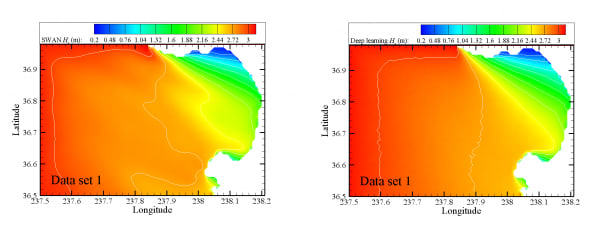
A key challenge in “learning” the correct representation of the data in machine learning approaches is selecting the correct topology for your model that best represents the data. One needs to determine the correct topology (at a basic level, the number of layers and nodes within the model or degree of nonlinearity that it is capable of resolving). An effective model needs to be sufficiently deep to model the nonlinearities in the data without ‘underfitting’ or ‘overfitting’ the training data.
A model that underfits the data is equivalent to trying to fit a straight line to a polynomial set of data points; it does not have sufficient degrees of freedom to track the data. An overfit model, on the other hand, provides too good a fit to the training data, or learns the data too well. This means that the noise or random fluctuations in the training data is also learned by the model and negatively impacts its predictive capabilities.
Is there anything else you’d like to add about this project?
This project presents a paradigm shift in wave forecasting, moving from a rule-based to a data-driven approach. The end result is an accurate forecast that takes seconds rather than hours to compute.
Forecasting using physics based models has a long and distinguished history that has enabled huge advances in both scientific understanding and operational decision-making. These models are built on our understanding of fundamental processes driving geoscientific processes gleaned from scientific theory, observation and empiricism.
We envision machine learning models complementing these existing, highly developed systems in a mutually beneficial way.
Machine learning models do not contain hard coded information about the system that they are studying and simply learn underlying relationships by processing large volumes of data. By combining both approaches we can train machine learning models with the outputs from physics based models.
This marries the accuracy and information provided by long-standing physics-based models with the comparatively nominal computational cost of machine learning approaches. The end-result is highly-accurate forecasts in a fraction of the time.
Engineers are trained to use data to make decisions and optimize construction and operation processes. In the future phase, we are interested to use the almost immediate forecasts provided by this framework to work with industry partners to better manage and optimize operations connected with marine-based businesses, such as shipping, aquaculture and offshore operations.
For more information, check out our article on Choosing the Right Turbulence Model for Your CFD Simulation and our eBook on Turbulence Models Offered by CFD Simulation Vendors.
